后缀数组是处理字符串的有力工具，设有长为 的字符串 ，则 表示字符串区间 在所有后缀中的按字典序从小到大排序的排名。而 表示排名为 的后缀的编号是哪一个。这两个数组显然互逆，即 rk[sa[i]]=sa[rk[i]]=irk[sa[i]]=sa[rk[i]]=i。借用 OI Wiki 的一张图来说明后缀数组。

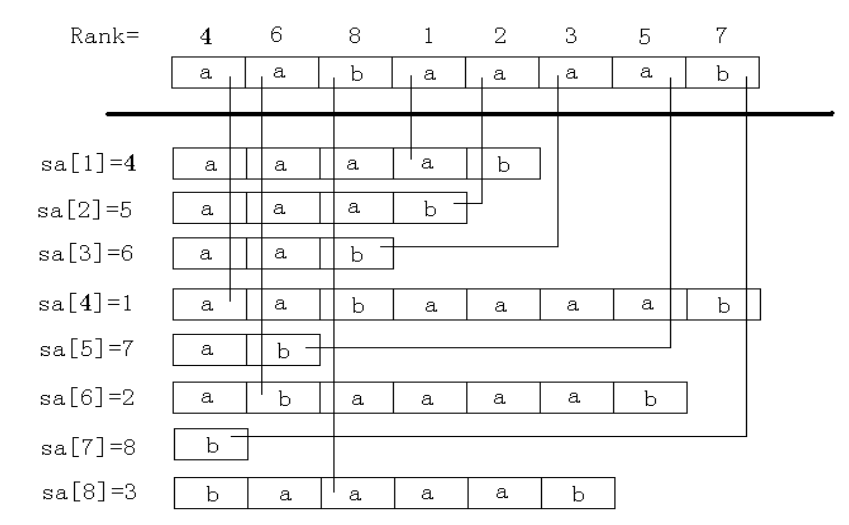
求后缀数组可使用 倍增+基数排序 在 的时间复杂度内完成。

height[i]height[i] 表示 sa[i]sa[i] 和 sa[i-1]sa[i-1] 所对应的后缀的最长公共前缀（即 LCP）。其具有以下性质：

• height[rk[i]]height[rk[i]] height[rk[i]-1]-1height[rk[i]-1]-1

📝 NOTE 考虑证明：

为了方便，将把 heightheight 简写为 。

当 height[rk[i]-1]height[rk[i]-1] 时，结论显然成立。

否则，不妨设 与 的 LCP 为 （其中 是字符， 是字符串），则 可表示为 ， 可表示为 ，因此 可表示为 （少了一个字符）。根据字典序的性质，我们知 后缀 后缀 。即 。

根据 heightheight 数组定义，知 后缀 必然在 和 之间，由字典序的排列性质知其必然至少有公共前缀 ，而 的长度就为 height[rk[i]-1]-1height[rk[i]-1]-1。