235 字
1 分钟
prufer 序列
Prufer 序列
对于一颗有编号的无根树,不妨设它有 个点,通过 prufer 序列,我们可以将它用唯一的长为 的序列来表示。而且对于任何一个长为 ,值域为 的整数序列,我们也可以把它转成对应的有编号无根树。即树与序列为双射关系,下面给出具体介绍。
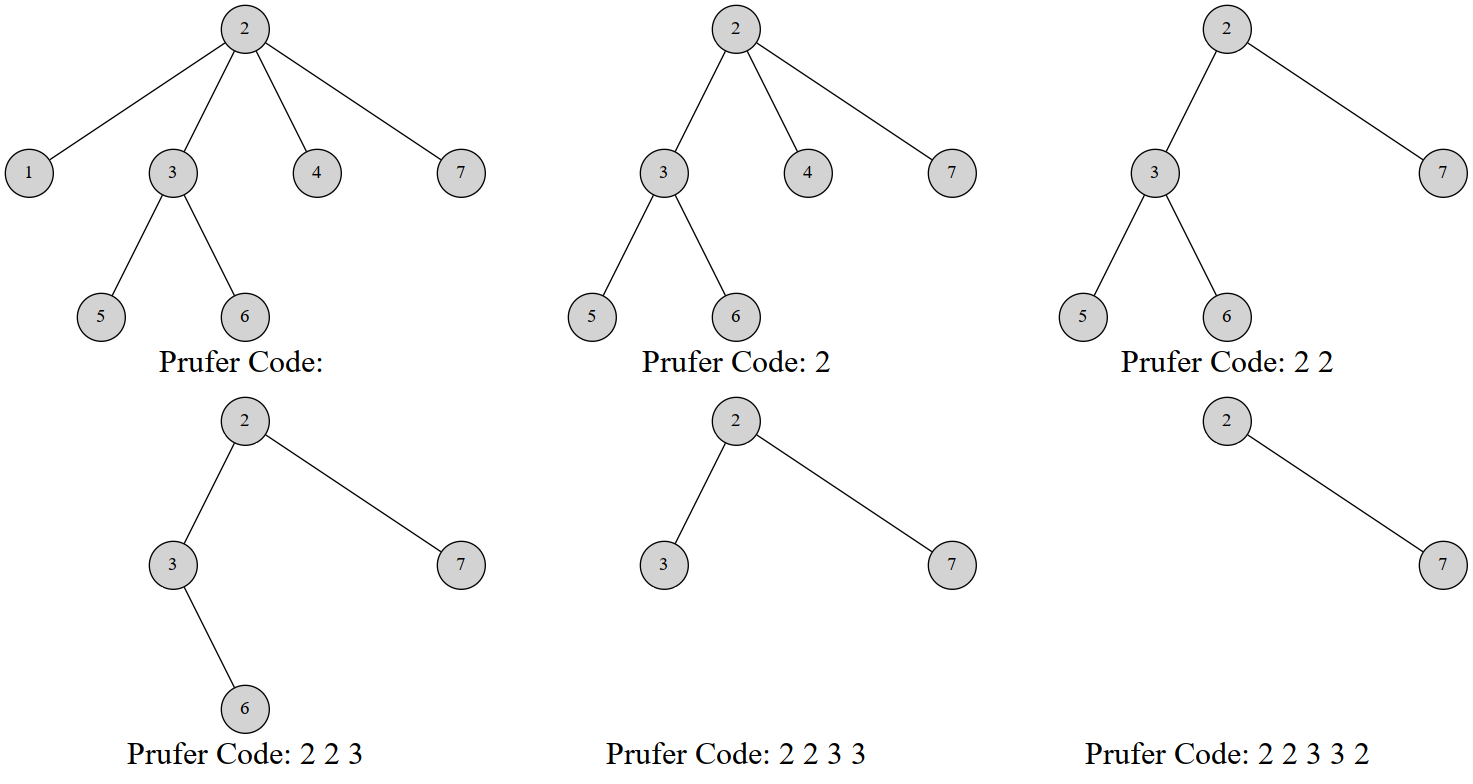
对树建立 Prufer 序列
- 找到该树的所有叶子结点
- 将编号最小的叶子节点取出,设其为 。
- 找到 相连的节点 。
- 将 加入 prufer 序列的末尾。
- 删去 ,递归该步骤,直至 prufer 序列中有 个元素。
💡 TIP 为什么不直到 个元素才停止?
因为第 个元素按照上述构造过程可以证明其一定为 ,将其加入序列无意义。
建立 prufer 序列过程(摘自 OI Wiki)
对 Prufer 序列建立树
📝 NOTE 性质:
- 序列中 元素的出现次数 其在原树上的度数减 。
- 在构造完 Prufer 序列后原树中会剩下两个结点,其中一个一定是编号最大的点 。
根据这个性质,我们可以找出原树中的所有叶子,按照从小到大排序,则最小的叶子一定与 Prufer 序列的第一个元素有一条边。然后将 Prufer 序列的的一个元素的度数 ,若 后为叶子,加入待处理序列中,递归处理即可。
放一个 OI Wiki 的链接。
因此,我们可以说明以下结论是成立的:
完全图 有 颗不同的无根生成树。
通过 Prufer 序列与树的一一对应关系,这个公式的正确容易说明。
💡 TIP 那有根树呢?
显然在一个无根树中,每个点都有可能做根节点,乘 即可。即最终答案为 。
